Prediction of non-exercise activity thermogenesis (NEAT) using multiple linear regression in healthy Korean adults: a preliminary study
Article information
Abstract
[Purpose]
This preliminary study aimed to develop a regression model to estimate the non-exercise activity thermogenesis (NEAT) of Korean adults using various easy-to-measure dependent variables.
[Methods]
NEAT was measured in 71 healthy adults (male n = 29; female n = 42). Statistical analysis was performed to develop a NEAT estimation regression model using the stepwise regression method.
[Results]
We confirmed that ageA, weightB, heart rate (HR)_averageC, weight × HR_averageD, weight × HR_sumE, systolic blood pressure (SBP) × HR_restF, fat mass ÷ height2G, gender × HR_averageH, and gender × weight × HR_sumI were important variables in various NEAT activity regression models. There was no significant difference between the measured NEAT values obtained using a metabolic gas analyzer and the predicted NEAT.
[Conclusion]
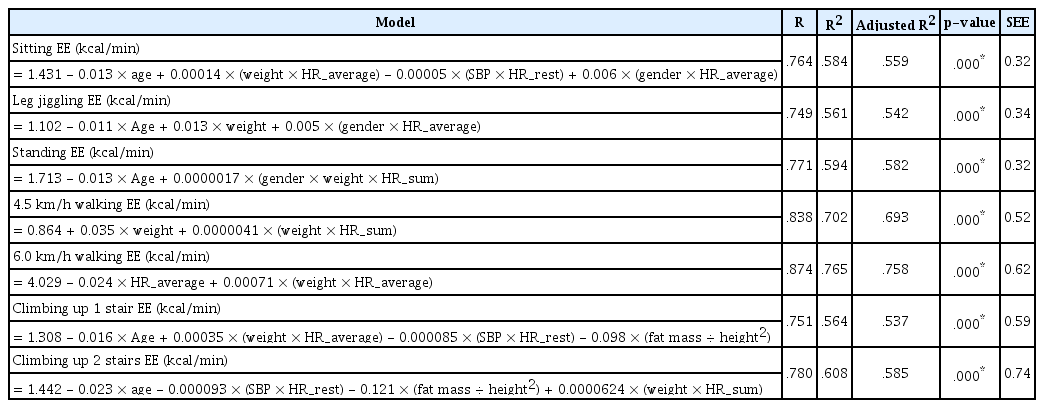
This preliminary study developed a regression model to estimate the NEAT in healthy Korean adults. The regression model was as follows: sitting = 1.431 - 0.013 × (A) + 0.00014 × (D) - 0.00005 × (F) + 0.006 × (H); leg jiggling = 1.102 - 0.011 × (A) + 0.013 × (B) + 0.005 × (H); standing = 1.713 - 0.013 × (A) + 0.0000017 × (I); 4.5 km/h walking = 0.864 + 0.035 × (B) + 0.0000041 × (E); 6.0 km/h walking = 4.029 - 0.024 × (C) + 0.00071 × (D); climbing up 1 stair = 1.308 - 0.016 × (A) + 0.00035 × (D) - 0.000085 × (F) - 0.098 × (G); and climbing up 2 stairs = 1.442 - 0.023 × (A) - 0.000093 × (F) - 0.121 × (G) + 0.0000624 × (E).
INTRODUCTION
In modern people, increased intake of high-calorie foods and imbalance in nutrient intake occur, and energy expenditure (EE) decreases due to a lack of physical activity and exercise [1]. Recently, due to social distancing during the novel coronavirus disease (COVID-19) pandemic, physical activity has become lesser than before, and sedentary behaviors such as television viewing time [2], computer activity, and time reclining or lying down are increasing. Studies report that decreased physical activity is not only associated with obesity [3,4], cardiovascular disease, and mortality but also causes obesity and various other conditions, such as cardiovascular disease, hypertension, diabetes, and cancer [5].
To prevent obesity and promote health, total EE (TEE) must be increased, and TEE is primarily composed of resting EE (REE), diet-induced thermogenesis (DIT), and physical activity-induced EE (AEE) [6,7]. REE is the minimum metabolic activity necessary to sustain life, accounting for approximately 60% of the TEE, and is highly related to body size, such as lean mass. DIT accounts for about 10% of the TEE by digestion, absorption, and autonomic nervous activity following conversion to intermediate metabolites after food intake, which does not vary significantly from person to person. Finally, AEE can be subdivided into exercise-related activity thermogenesis (EAT) and non-exercise activity thermogenesis (NEAT), accounting for approximately 30% or more of the TEE [8,9].
REE and DIT are relatively constant, whereas AEE is highly versatile. In general, the EAT method has most commonly been used to increase TEE, but recently, NEAT has been shown to be as effective at energy consumption as exercise [10]. NEAT includes the EE of all physical activities, except voluntary activities such as exercise, and can be used in various ways related to work and leisure [11]. In previous studies, sedentary people accounted for 6–10% of TEE, while active people accounted for more than 50%, and physical activities such as shaking legs, cleaning, walking, and climbing stairs consumed 20% more energy than at rest [12,13]. As such, NEAT can increase the EE of daily activities and is considered a good way to improve health. In addition, the need for NEAT is growing during the COVID-19 pandemic, where external activities are limited, and it is essential to measure and evaluate NEAT accurately.
The first method to determine NEAT is by measuring and evaluating an individual’s physical activity, amount of regular exercise, and occupational activity intensity [13]. The advantage of this method is that it can collect data without special measuring equipment, but it is known to be inaccurate due to individual variations. The second method is to predict the amount of activity by collecting the intensity, duration, and frequency of physical activity using an accelerometer [14]. It is convenient to use in the field; however, it does not accurately reflect the amount of EE of special situations, such as walking with an object or walking uphill. The third method measures EE by analyzing oxygen and carbon dioxide concentrations with a breathing gas analyzer [15]. Although the accuracy is high, it is not suitable for large-scale research because it is costly and time-consuming. Lastly, the most standardized method of measuring EE is by ingesting water, using the isotope measurement method, and substituting it into the formula using the amount removed from the body over time [9]. It is difficult to accurately measure the intensity, frequency, and EE consistently.
As described above, there are various methods for analyzing NEAT. However, most of the measured values are obtained through laboratory measurements; thus, it is difficult to apply them to the field [16,17]. Therefore, it is vital to develop a simple and accurate EE estimation equation to measure and evaluate various NEAT activities. Currently, some studies have developed a regression model using height, age, weight, and heart rate (HR) for EE during exercise and rest. However, almost no studies at home or abroad have presented a regression model for estimating EE according to various NEAT activities. Therefore, it is essential to develop a regression model using multiple dependent variables for NEAT.
Thus, this study provides a regression model for predicting NEAT EE by measuring EE during various NEAT activities in Korean adults (male and female), making it easy to apply in public health programs and the field.
METHODS
Subjects
A total of 71 healthy adults (male = 29; female = 42) were included in the present study (Table 1). Subjects who met one or more of the following exclusion criteria were not eligible to participate in the study: unstable angina, recent cardiac infarction (4 weeks), uncompensated heart failure, severe valvular illness, pulmonary disease, uncontrolled hypertension, kidney failure, orthopedic/neurological limitations, cardiomyopathy, planned surgery during the research period, reluctance to sign the consent form, drug or alcohol abuse, or involvement in another study. There was also no history of an orthopedic disease or other medical issues over the past year in the pre-screening surveys. All subjects were fully acquainted with the nature of the study and informed of the experimental risks before signing a written consent form to participate. It was explicitly stated that the subjects could withdraw from the study at any point. The researchers fully explained their pretest research and received voluntary consent. All study procedures were approved by the Institutional Review Board of Konkuk University (7001355-201903-HR-305) in Korea and were conducted in accordance with the Declaration of Helsinki.
Experimental design
All subjects were required to avoid strenuous exercise for 48 h and arrive at the laboratory early in the morning (8:00 AM) after overnight fasting (≥ 8 h) and rested for 30 min. Next, body composition, blood pressure, and resting HR were measured, followed by a standardized breakfast (2 pieces of bread (200 kcal), 1 boiled egg (80 kcal), 1 cup of orange juice (120 kcal), and 1 cup of water). The subjects rested comfortably after breakfast and participated in the experiment 2 h later.
Body composition
Body height, body mass index (BMI), body weight, free fat mass (FFM), fat mass, and percent body fat were measured using bioelectrical impedance analysis equipment (InBody 770, InBody, Seoul, Korea). The participants were asked to wear light clothing and remove metal items and were measured standing upright and barefoot on the machine platform, placing their feet on the electrode of the platform, while their hands gripped the wires on the handles.
Blood pressure and resting HR
After all the subjects were sufficiently rested for more than 30 min, their blood pressure (systolic blood pressure [SBP] and diastolic blood pressure [DBP]) were measured twice using an autonomic blood pressure monitor (HBP9020, Omron, Tokyo, Japan), and the average value was used for analysis. The blood pressure parameters measured were SBP, DBP, mean arterial pressure (MAP = DBP + PP/3), pulse pressure (PP = SBP - DBP), and rate pressure product (RPP = SBP × HR). The resting HR was measured using an autonomic HR monitor (V800, Polar, Helsinki, Finland).
NEAT measurement
NEAT was measured by indirect calorimetry using a wearable metabolic gas analyzer (K5, Cosmed, Rome, Italy). Calibration was performed using calibration gas (16% O2 and 5% CO2) before the measurements. The measurement room had controlled humidity (50%) and temperature (23 ± 1 °C). Sitting, leg jiggling, standing, and walking were performed for 10 min each, and walking was performed on a treadmill (S25T, STEX, Seoul, Korea) at a speed of 4.5 km/h and 6.0 km/h. Stair climbing was performed with a gas analyzer and a stair height of 20 cm stepmill (StairMaster Gauntlet, Core Health, and Fitness, Washington, D.C.), and climbing up one stair and climbing up two stairs was carried out for 1 min each. After the measurement of each item was completed, sufficient rest was provided, and when the energy metabolism returned to the stable level, the measurement was started again [13,17].
Statistical analysis
The means and standard deviations were calculated for all the measured parameters. The Shapiro-Wilk test verified the normal distribution of all outcome variables. To perform the linear regression analysis, we verified the independent variables by checking the regression coefficient (β-value). Regression analysis using the stepwise method was used to predict NEAT based on sex, age, height, weight, BMI, FFM, fat mass, percent body fat, SBP, DBP, MAP, PP, RPP, HR_rest, HR_average, and HR_sum. A two-tailed Student’s paired t-test was used to detect the differences between the measured and predicted NEAT. Bias was calculated as the difference between the measured and predicted NEAT values. The authors rigorously conformed to the basic assumptions of a regression model (linearity, independence, continuity, normality, homoscedasticity, autocorrelation, and outlier). Statistical Package for the Social Sciences (SPSS) version 25.0 (IBM Corporation, Armonk, NY, USA) was used for the statistical analysis, and the level of significance (p-value) was set at 0.05.
RESULTS
Correlation between dependent variables and measured NEAT
To delete outlier data, the absolute value of the standard residual was checked as ≥ 3, and a stepwise method was used to estimate the regression model. To use only the variables with a large influence on each NEAT item in the regression model, gender, age, height, weight, BMI, FFM, fat mass, percent body fat, SBP, DBP, MAP, PP, RPP, HR_rest, HR_average, HR_sum, and various interactions related to HR were used as variables to explain NEAT. The correlations between the measured NEAT and the dependent variables are presented in Table 2.
Significance of regression models and the independent variables
We verified the significance of each model using the F-test and used a t-test to verify the significance of the regression coefficients of the independent variables. The results of the regression analysis for estimating the NEAT for each motion based on the results of the exploratory data analysis are shown in Table 3. The regression coefficients of the selected independent variables (age, weight, HR_average, weight × HR_average, weight × HR_sum, SBP × HR_rest, fat ÷ height2, gender × HR_average, and gender × weight × HR_sum) for each motion were statistically significant when the integrated regression model was developed using the stepwise method.
Performance evaluation of regression models and regression equations
The coefficients of determination (R2), adjusted coefficients of determination (adjusted R2), and standard errors of estimates (SEE) were calculated for the regression model. The mean explanatory power of the sitting EE regression models developed by age, weight × HR_average, SBP × HR_rest, and Gender × HR_average were 58.4% (R2) and 55.9% (adjusted R2), while the mean SEE was 0.32. The mean explanatory power of the leg jiggling EE regression models developed by age, weight, and gender × HR_average were 56.1% (R2) and 54.2% (adjusted R2), and the mean SEE was 0.34 kcal/min. The mean explanatory power of the standing EE regression models developed by age and gender × weight × HR_sum was 59.4% (R2) and 58.2% (adjusted R2), and the mean SEE was 0.32. The mean explanatory power of the 4.5 km/h walking EE regression models developed by weight and weight × HR_sum was 70.2% (R2) and 69.3% (adjusted R2), and the mean SEE was 0.52 kcal/min. The mean explanatory power of the 6.0 km/h walking EE regression models developed by HR_average and weight × HR_average was 76.5% (R2) and 75.8% (adjusted R2), and the mean SEE was 0.62 kcal/min. The mean explanatory power of the climbing-up-1-stair EE regression models developed by age, weight × HR_average, SBP × HR_rest, and fat ÷ height2 were 56.4% (R2) and 53.7% (adjusted R2), and the mean SEE was 0.59 kcal/min. The mean explanatory power of the climbing-up-2-stairs EE regression models developed by age, SBP × HR_rest, fat mass ÷ height2, and weight × HR_sum was 60.8% (R2) and 58.5% (adjusted R2), and the mean SEE were 0.74 kcal/min (Table 4).
Difference between measured and predicted NEAT of Korean adults
In the present study, there was no significant difference between NEAT for each motion measured using a metabolic gas analyzer and NEAT for each motion predicted by the equation. The mean bias between the measured and predicted NEAT equations were as follows: sitting = 0.003 kcal/min; leg jiggling = 0.004 kcal/min; standing + 0.003 kcal/min; 4.5 km/h walking - 0.005 kcal/min; 6.0 km/h walking + 0.003 kcal/min; climbing up 1 stair + 0.007 kcal/min; and climbing up 2 stairs + 0.004 kcal/min, respectively (Table 5). The measured and predicted NEAT showed a similar average value, and their correlation coefficients also showed a significant correlation (sitting: R = 0.764, p = 0.000; leg jiggling: R = 0.749, p = 0.000; standing: R = 0.771, p = 0.000; 4.5 km/h walking: R = 0.838, p = 0.000; 6.0 km/h walking: R = 0.874, p = 0.000; climbing up 1 stairs: R = 0.751, p = 0.000; and climbing up 2 stairs: R = 0.780, p = 0.000).
DISCUSSION
Oxygen consumption (VO2) is considered the most accurate variable for measuring the EE of physical activity and can be measured directly in the laboratory using a metabolic cart or respiratory gas analyzer. Portable devices are available for field measurements, but only for a limited period of time and with a limited number of targets. Therefore, efforts are being made to find a more feasible way to estimate VO2 in field studies [18,19]. In particular, it has been reported that individual characteristics such as age, sex, and weight should be considered. However, easily measurable HR is used as a way to estimate VO2 [20]. Most of the studies using HR have been used in regression models that estimate EE of exercise in active energies. None of the regression models that estimate the EE of NEAT has been studied using HR. Therefore, we suggest ways to estimate NEAT EE using HR.
In this work, a preliminary study was conducted to develop a regression model for estimating the EE of various NEAT activities in Korean adults using various dependent variables that are easy to measure. Based on the collected data, our study developed a regression model of NEAT for each motion (sitting EE = 1.431 - 0.013 × age + 0.00014 × (weight × HR_average) - 0.00005 × (SBP × HR_rest) + 0.006 × (gender × HR_average); leg jiggling EE = 1.102 - 0.011 × age + 0.013 × weight + 0.005 × (gender × HR_average); standing EE = 1.713 - 0.013 × Age + 0.0000017 × (gender × weight × HR_sum); 4.5 km/h walking EE = 0.864 + 0.035 × weight + 0.0000041 × (weight × HR_sum); 6.0 km/h walking EE = 4.029 - 0.024 × HR_average + 0.00071 × (weight × HR_average); climbing up 1 stair EE = 1.308 - 0.016 × age + 0.00035 × (weight × HR_average) - 0.000085 × (SBP × HR_rest) - 0.098 × (fat mass ÷ height2); and climbing up 2 stairs EE = 1.442 - 0.023 × age - 0.000093 × (SBP × HR_rest) - 0.121 × (fat mass ÷ height2) + 0.0000624 × (weight × HR_sum)).
Looking at the correlation between various NEAT activity EE and dependent variables in Korean adults, the variables related to HR and various measured variables showed a significant correlation with NEAT (e.g., age; weight; HR_ average; weight × HR_average; weight × HR_sum; SBP × HR_rest; fat mass ÷ height2 ; gender × HR_average; and gender × weight × HR_sum) for each motion. Previously, Park et al. [21] developed a regression model of the EE of an exercise stress test using the HR of college students in their 20s (EE 1 (cal/min) = 100.127 + (s × - 8577.731) + (w × 106.729) + (h × 12.580) + ((s × w) × 113.209) + ((w × h) × 38.847) + ((s × h) × 1.251) + ((s × h × w) × - 0.23), where s = sex : male-1, female-0, h = heart rate : beat/min, w = weight: kg, R2 = 0.85; and EE 2 (cal/min) = 15289.276 + (s × 117.083) + (w × 102.905) + (h × 1883.398), where s = sex : male-1, female-0, h = heart rate : beat/min, w = weight : kg, R2 = 0.82). In addition, the studies of Charlot et al. [22] developed a regression model to estimate the EE of exercise using HR (EE [kcal · h−1] = 171.62 + 6.87 × HR (bpm) + 3.99 × height (cm) + 2.30 × weight (kg) −139.89 × sex (1 or 2) − 4.26 × resting HR (bpm) − 4.87 × HRmax (bpm), R2 = 0.879). Both estimation expressions show a high regression model with a correlation coefficient of 0.80 or higher, but it was a study to estimate the EE of exercise rather than NEAT activity.
Other studies, such as Bouchard and Trudeau [23] and Levine et al. [17], used an accelerometer to measure EE and showed a high correlation between the actual measured value but underestimated according to exercise intensity or overestimated. As in this study, studies on estimating EE using HR in various NEAT activities are insufficient; thus, many studies should be conducted in the future. Estimating EE using HR is very linear, regardless of age or gender, and is effective against estimating energy due to low in-person variability. However, errors in measurement methods and predictions have also been reported, and careful attention is needed to interpret the results [24]. Although it is judged that more accurate measurements should be made because of the nature of NEAT with low exercise intensity, it is convenient to use a regression model for each NEAT activity that can be easily applied by ordinary people to effectively manage their health.
In conclusion, through preliminary experiments, we developed a regression model using HR and multiple variables to estimate the EE of various NEAT activities in healthy Korean adults. The developed model is as follows: sitting EE = 1.431 - 0.013 × age + 0.00014 × (weight × HR_average) - 0.00005 × (SBP × HR_rest) + 0.006 × (gender × HR_average); leg jiggling EE = 1.102 - 0.011 × age + 0.013 × weight + 0.005 × (gender × HR_average); standing EE = 1.713 - 0.013 × age + 0.0000017 × (gender × weight × HR_sum); 4.5 km/h walking EE = 0.864 + 0.035 × weight + 0.0000041 × (weight × HR_sum); 6.0 km/h walking EE = 4.029 - 0.024 × HR_average + 0.00071 × (weight × HR_average); climbing up 1 stair EE = 1.308 - 0.016 × age + 0.00035 × (weight × HR_average) - 0.000085 × (SBP × HR_rest) - 0.098 × (fat mass ÷ height2); and climbing up 2 stairs EE = 1.442 - 0.023 × age - 0.000093 × (SBP × HR_rest) - 0.121 × (fat mass ÷ height2) + 0.0000624 × (weight × HR_sum). Bias between estimated NEAT and measured NEAT (sitting = - 0.003; leg jiggling = 0.004; standing = 0.003; 4.5 km/h walking = - 0.005; 6.0 km/h walking = 0.003; climbing up 1 stair = 0.007; and climbing up 2 stairs = 0.004) and correlation (sitting: R = 0.764; leg jiggling: R = 0.749; standing: R = 0.771; 4.5 km/h walking: R = 0.838; 6.0 km/h walking: R = 0.874; climbing up 1 stair: R = 0.751; and climbing up 2 stairs: R = 0.780) was reasonable.
However, this study has limitations as a preliminary study. The sample size was small, we were unable to develop regression models for gender, and validity tests could not be performed. Therefore, further research is required to overcome these limitations.
Acknowledgements
This work was supported by the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF-2019S1A5B8099542).